Le carré magique
Principe
En mathématiques, un carré magique d’ordre n est composé de n2 entiers strictement positifs, écrits sous la forme d’un tableau carré. Ces nombres sont disposés de sorte que leurs sommes sur chaque ligne, sur chaque colonne et sur chaque diagonale principale soient égales. On nomme alors constante magique (et parfois densité) la valeur de ces sommes (n * (n2 + 1)/ 2).
Un carré magique normal est un cas particulier de carré magique, constitué de tous les nombres entiers de 1 à n2, où n est l’ordre du carré. (source : Wikipedia.org)

et de constante magique 15.
Somme des termes d'une ligne = somme des termes d'une colonne = somme des termes d'une diagonale principale = 3 * (32 + 1) = 15.
Plusieurs algorithmes permettent de construire des carrés magiques d'ordre n impair. Voici l'un d'eux :
Algorithme de construction d’un carré magique d’ordre impair
Etape 1:
On commence par initialiser tous les éléments du tableau à zéro. L'initialisation à zéro de tous les éléments du carré permettra ultérieurement de déduire si la case pointée est libre ou non.
Etape 2:
Le chiffre 1 est placé dans la case au milieu de la dernière ligne du carré.
Etape 3:
Une fois qu'une case a été remplie, on en choisit une autre en effectuant, par rapport à la case qui vient d'être remplie précédemment, deux mouvements successifs :
- l'un horizontal vers la case de droite
- l'autre vertical d'une case vers le haut
Si i est l'indice de ligne et j l'indice de colonne, ce déplacement s'obtient en effectuant i = i+1 et j = j+1. Deux cas peuvent alors se présenter:
- La case atteinte est libre, on y place alors le nombre suivant.
- La case atteinte est déjà remplie, on en choisit une autre en effectuant un déplacement vertical vers le haut à partir de la case de départ.
Etape 4:
La loi de progression mentionnée ci-dessus entraînera tôt ou tard une sortie hors des limites du carré défini. Dès qu'un déplacement oblige à sortir du carré, on se place dans la case correspondante du bord opposé et on continue à effectuer la suite des déplacements.
On peut interpréter cette règle d'une autre manière, en considérant simplement que le carré est, pour chaque dimension, placé sur un cylindre de telle sorte que la ligne du bas est située immédiatement au- dessus de celle du haut, que la colonne de droite est située à gauche de la première colonne, et réciproquement pour la colonne de gauche.
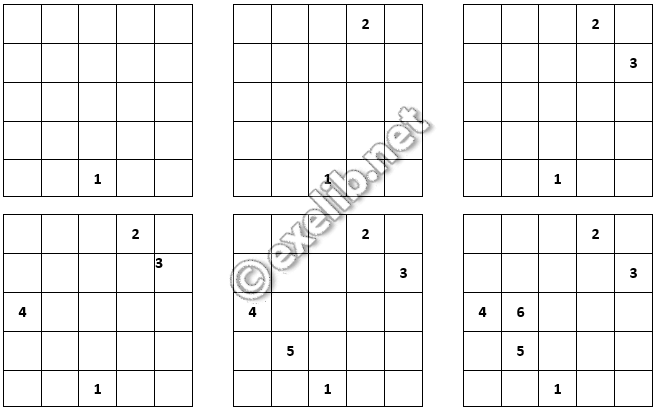
Le résultat final est un carré magique dont la constante est 65.
| 11 | 18 | 25 | 2 | 9 |
| 10 | 12 | 19 | 21 | 3 |
| 4 | 6 | 13 | 20 | 22 |
| 23 | 5 | 7 | 14 | 16 |
| 17 | 24 | 1 | 8 | 15 |
La création des carrés magiques d’ordre pair est plus difficile.
Indications pour la programmation
- On n'effectuera pas le calcul si l'ordre n demandé n'est pas impair.
- On se limite à un ordre tel que la visualisation reste possible.
- Place le chiffre 1 dans la case d’indice (n, (n + 1)/2).
- Si une case n’est pas vide, le nombre suivant est placé à la case d’indice (i-1, j).
- Si un indice est supérieur à n il est ramené à 1.
Fonctions à réaliser
Le programme principal devra impérativement appeler au moins 2 fonctions :
- Une première fonction qui consiste à générer le carré magique de l'ordre spécifié en suivant l'algorithme donné précédemment.
- Une deuxième fonction ayant pour objectif de réaliser la visualisation à l'écran du carré magique résultant des calculs précédents.
- Réaliser une fonction permettant de vérifier si le carré est bien magique.
- Améliorer la procédure d'affichage tel que celui-ci puisse se réaliser en temps réel. Ainsi, on doit pouvoir observer le remplissage du carré magique au fur et à mesure qu'un nombre a été introduit dans le tableau.
Fonction d'initialisation du tableau:
void initialiser(int t[20][20], int n){
int i, j;
for(i=1; i<=n; i++){
for(j=1; j<=n; j++){
t[i][j] = 0;
}
}
t[n][(n+1)/2] = 1;
}
Fonction récursive qui permet de construire le carre magique:
void placer(int t[20][20], int n, int i, int j){
//afficher(t,n);
if(est_magique(t,n)){
return;
}
else{
int k = t[i][j];
int i1 = i;
int j1 = j;
if(i == n){
i = 0;
}
if(j == n){
j = 0;
}
if(t[i+1][j+1] == 0){
t[i + 1][j + 1] = k + 1;
placer(t, n, i+1, j+1);
}
else{
t[i1 - 1][j1] = k + 1;
placer(t, n, i1-1, j1);
}
}
}
Fonction d'affichage:
void afficher(int t[20][20], int n){
int i, j;
printf("\n\n");
for(i=1; i<=n; i++){
for(j=1; j<=n; j++){
printf("%d\t", t[i][j]);
}
printf("\n");
}
}
Fonction qui vérifie si le carré est bien magique:
int est_magique(int t[20][20], int n){
int i, j;
int s = 0;
int const_magique = n * (n * n + 1) / 2;
//Somme des lignes
for(i=1; i<=n; i++){
s = 0;
for(j=1; j<=n; j++){
s = s + t[i][j];
}
if(s != const_magique){
return 0;
}
}
//Somme des colonnes
for(i=1; i<=n; i++){
s = 0;
for(j=1; j<=n; j++){
s = s + t[j][i];
}
if(s != const_magique){
return 0;
}
}
//Somme des diagonales
s = 0;
for(i=1; i<=n; i++){
s = s + t[i][i];
}
if(s != const_magique){
return 0;
}
s = 0;
for(i=1; i<=n; i++){
s = s + t[i][n-i+1];
}
if(s != const_magique){
return 0;
}
return 1;
}
Programme complet:
//Auteur: IDMANSOUR
//Copyright: Exelib.net
#include<stdio.h>
//Fonction d'initialisation du tableau
void initialiser(int t[20][20], int n){
int i, j;
for(i=1; i<=n; i++){
for(j=1; j<=n; j++){
t[i][j] = 0;
}
}
t[n][(n+1)/2] = 1;
}
//Fonction récursive qui permet de construire le carre magique
void placer(int t[20][20], int n, int i, int j){
//afficher(t,n);
if(est_magique(t,n)){
return;
}
else{
int k = t[i][j];
int i1 = i;
int j1 = j;
if(i == n){
i = 0;
}
if(j == n){
j = 0;
}
if(t[i+1][j+1] == 0){
t[i + 1][j + 1] = k + 1;
placer(t, n, i+1, j+1);
}
else{
t[i1 - 1][j1] = k + 1;
placer(t, n, i1-1, j1);
}
}
}
void afficher(int t[20][20], int n){
int i, j;
printf("\n\n");
for(i=1; i<=n; i++){
for(j=1; j<=n; j++){
printf("%d\t", t[i][j]);
}
printf("\n");
}
}
//Fonction qui test si le tableau passé en paramètre est un carré magique
int est_magique(int t[20][20], int n){
int i, j;
int s = 0;
int const_magique = n * (n * n + 1) / 2;
//Somme des lignes
for(i=1; i<=n; i++){
s = 0;
for(j=1; j<=n; j++){
s = s + t[i][j];
}
if(s != const_magique){
return 0;
}
}
//Somme des colonnes
for(i=1; i<=n; i++){
s = 0;
for(j=1; j<=n; j++){
s = s + t[j][i];
}
if(s != const_magique){
return 0;
}
}
//Somme des diagonales
s = 0;
for(i=1; i<=n; i++){
s = s + t[i][i];
}
if(s != const_magique){
return 0;
}
s = 0;
for(i=1; i<=n; i++){
s = s + t[i][n-i+1];
}
if(s != const_magique){
return 0;
}
return 1;
}
main(){
int n, A[20][20];
printf("Donner l'ordre de votre carre magique: ");
scanf("%d", &n);
//n pair
if(n % 2 == 0){
printf("Veuillez entrer un nombre impair!");
return;
}
initialiser(A, n);
placer(A, n, n , (n+1)/2);
printf("Le carre magique d'ordre %d : ", n);
afficher(A, n);
if(est_magique(A, n)){
puts("\nLe carre genere est bien un carre magique :)");
}
else{
puts("\nLe carre genere n\'est pas magique! (Algorithme incorrect) :(");
}
}
Dans ce programme, les indices du tableau commencent par 0 au lieu de 1. Donc si un indice dépasse les bornes du tableau (indice n-1) on le ramène à 0.